1. Web
  2. Web API
  3. WebGL: 網頁的 2D 和 3D 圖形
  4. WebGL 模型檢視投影

WebGL 模型檢視投影

本文探討如何在 WebGL 專案中獲取資料，並將其投影到適當的空間以顯示在螢幕上。它假設讀者瞭解使用平移、縮放和旋轉矩陣進行基本矩陣數學運算的知識。它解釋了在組合 3D 場景時通常使用的三個核心矩陣：模型矩陣、檢視矩陣和投影矩陣。

模型矩陣、檢視矩陣和投影矩陣

WebGL 中點和多邊形在空間中的單獨變換由基本的變換矩陣（如平移、縮放和旋轉）處理。這些矩陣可以組合在一起，並以特殊方式分組，以便它們可用於渲染複雜的 3D 場景。這些組合矩陣最終將原始模型資料移動到名為裁剪空間的特殊座標空間中。這是一個 2 個單位寬的立方體，以 (0,0,0) 為中心，角點範圍從 (-1,-1,-1) 到 (1,1,1)。這個裁剪空間被壓縮成 2D 空間並光柵化成影像。

下面討論的第一個矩陣是模型矩陣，它定義瞭如何獲取原始模型資料並在 3D 世界空間中移動它。投影矩陣用於將世界空間座標轉換為裁剪空間座標。一個常用的投影矩陣，即透視投影矩陣，用於模擬典型相機作為 3D 虛擬世界中觀察者的效果。檢視矩陣負責移動場景中的物件，以模擬相機位置的變化，從而改變觀察者當前能夠看到的內容。

以下部分深入探討了模型矩陣、檢視矩陣和投影矩陣背後的思想和實現。這些矩陣是資料在螢幕上移動的核心，並且是超越單個框架和引擎的概念。

裁剪空間

在 WebGL 程式中，資料通常以其自己的座標系上傳到 GPU，然後頂點著色器將這些點轉換成一個稱為裁剪空間的特殊座標系。任何超出裁剪空間的資料都將被裁剪掉，不予渲染。但是，如果一個三角形橫跨此空間的邊界，則它將被分割成新的三角形，並且只保留新三角形在裁剪空間中的部分。

A 3d graph showing clip space in WebGL.

上面的圖形是所有點必須適合的裁剪空間的視覺化。它是一個邊長為兩個單位的立方體，一個角在 (-1,-1,-1)，對角在 (1,1,1)。立方體的中心是點 (0,0,0)。裁剪空間使用的這個 8 立方米的座標系稱為歸一化裝置座標 (NDC)。你在研究和使用 WebGL 程式碼時可能會不時遇到這個術語。

對於本節，我們將直接將資料放入裁剪座標系。通常使用任意座標系中的模型資料，然後使用矩陣對其進行變換，將模型座標轉換為裁剪空間座標系。對於這個示例，最容易透過使用範圍從 (-1,-1,-1) 到 (1,1,1) 的模型座標值來說明裁剪空間的工作原理。下面的程式碼將建立 2 個三角形，它們將在螢幕上繪製一個正方形。正方形中的 Z 深度決定了當正方形共享相同空間時哪個被繪製在上面。較小的 Z 值被渲染在較大的 Z 值之上。

WebGLBox 示例

此示例將建立一個自定義的 WebGLBox 物件，它將在螢幕上繪製一個 2D 框。它被實現為一個類，其中包含一個建構函式和一個 draw() 方法來在螢幕上繪製一個框。

js
class WebGLBox {
  canvas = document.getElementById("canvas");
  gl = this.canvas.getContext("webgl");
  webglProgram = createWebGLProgramFromIds(
    this.gl,
    "vertex-shader",
    "fragment-shader",
  );
  positionLocation;
  colorLocation;
  constructor() {
    const gl = this.gl;

    // Setup a WebGL program
    gl.useProgram(this.webglProgram);

    // Save the attribute and uniform locations
    this.positionLocation = gl.getAttribLocation(this.webglProgram, "position");
    this.colorLocation = gl.getUniformLocation(this.webglProgram, "vColor");

    // Tell WebGL to test the depth when drawing, so if a square is behind
    // another square it won't be drawn
    gl.enable(gl.DEPTH_TEST);
  }
  draw(settings) {
    // Create some attribute data; these are the triangles that will end being
    // drawn to the screen. There are two that form a square.

    // prettier-ignore
    const data = new Float32Array([
      // Triangle 1
      settings.left, settings.bottom, settings.depth,
      settings.right, settings.bottom, settings.depth,
      settings.left, settings.top, settings.depth,

      // Triangle 2
      settings.left, settings.top, settings.depth,
      settings.right, settings.bottom, settings.depth,
      settings.right, settings.top, settings.depth,
    ]);

    // Use WebGL to draw this onto the screen.

    // Performance Note: Creating a new array buffer for every draw call is slow.
    // This function is for illustration purposes only.

    const gl = this.gl;

    // Create a buffer and bind the data
    const buffer = gl.createBuffer();
    gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
    gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);

    // Setup the pointer to our attribute data (the triangles)
    gl.enableVertexAttribArray(this.positionLocation);
    gl.vertexAttribPointer(this.positionLocation, 3, gl.FLOAT, false, 0, 0);

    // Setup the color uniform that will be shared across all triangles
    gl.uniform4fv(this.colorLocation, settings.color);

    // Draw the triangles to the screen
    gl.drawArrays(gl.TRIANGLES, 0, 6);
  }
}

著色器是使用 GLSL 編寫的程式碼片段，它們獲取我們的資料點並最終將它們渲染到螢幕上。為方便起見，這些著色器儲存在 <script> 元素中，並透過自定義函式 createWebGLProgramFromIds() 引入程式。此函式處理獲取一些 GLSL 原始碼並將其編譯為 WebGL 程式的基本操作。它需要三個引數——渲染程式的上下文、包含頂點著色器的 <script> 元素的 ID，以及包含片段著色器的 <script> 元素的 ID。此函式在此處不詳細解釋；如果你想檢視其實現，請點選程式碼塊上的“播放”。頂點著色器定位頂點，片段著色器為每個畫素著色。

首先看一下將在螢幕上移動頂點的頂點著色器

glsl
// The individual position vertex
attribute vec3 position;

void main() {
  // the gl_Position is the final position in clip space after the vertex shader modifies it
  gl_Position = vec4(position, 1.0);
}

接下來，要將資料實際光柵化為畫素，片段著色器以每個畫素為基礎評估所有內容，並設定單個顏色。GPU 為它需要渲染的每個畫素呼叫著色器函式；著色器的任務是返回用於該畫素的顏色。

glsl
precision mediump float;
uniform vec4 vColor;

void main() {
  gl_FragColor = vColor;
}

包含這些設定後，是時候直接使用裁剪空間座標繪製到螢幕了。

js
const box = new WebGLBox();

首先在中間繪製一個紅色框。

js
box.draw({
  top: 0.5, // x
  bottom: -0.5, // x
  left: -0.5, // y
  right: 0.5, // y

  depth: 0, // z
  color: [1, 0.4, 0.4, 1], // red
});

接下來，在紅色框的上方和後面繪製一個綠色框。

js
box.draw({
  top: 0.9, // x
  bottom: 0, // x
  left: -0.9, // y
  right: 0.9, // y

  depth: 0.5, // z
  color: [0.4, 1, 0.4, 1], // green
});

最後，為了演示裁剪確實正在發生，此框未被繪製，因為它完全超出裁剪空間。深度超出 -1.0 到 1.0 的範圍。

js
box.draw({
  top: 1, // x
  bottom: -1, // x
  left: -1, // y
  right: 1, // y

  depth: -1.5, // z
  color: [0.4, 0.4, 1, 1], // blue
});

結果

練習

此時一個有用的練習是移動裁剪空間中的框，透過改變程式碼來感受點如何在裁剪空間中被裁剪和移動。嘗試繪製一個像帶背景的方塊笑臉的圖片。

齊次座標

前一個裁剪空間頂點著色器的主要行包含此程式碼

glsl
gl_Position = vec4(position, 1.0);

position 變數在 draw() 方法中定義，並作為屬性傳遞到著色器。這是一個三維點，但最終透過管道傳遞的 gl_Position 變數實際上是四維的——不是 (x, y, z)，而是 (x, y, z, w)。z 之後沒有字母，因此按照慣例，這個第四維度標記為 w。在上面的示例中，w 座標設定為 1.0。

顯而易見的問題是“為什麼多了一個維度？”事實證明，這個附加維度允許許多操縱 3D 資料的好技術。這個附加維度將透視概念引入座標系；有了它，我們可以將 3D 座標對映到 2D 空間——從而允許兩條平行線在它們向遠處後退時相交。w 的值用作座標其他分量的除數，因此 x、y 和 z 的真實值計算為 x/w、y/w 和 z/w（然後 w 也成為 w/w，變為 1）。

一個三維點在典型的笛卡爾座標系中定義。新增的第四維將此點更改為齊次座標。它仍然代表 3D 空間中的一個點，並且可以很容易地透過一對簡單函式演示如何構造這種型別的座標。

js
function cartesianToHomogeneous(point) {
  let x = point[0];
  let y = point[1];
  let z = point[2];

  return [x, y, z, 1];
}

function homogeneousToCartesian(point) {
  let x = point[0];
  let y = point[1];
  let z = point[2];
  let w = point[3];

  return [x / w, y / w, z / w];
}

如前所述，並在上述函式中所示，w 分量除以 x、y 和 z 分量。當 w 分量是非零實數時，齊次座標很容易轉換回笛卡爾空間中的正常點。現在，如果 w 分量為零會發生什麼？在 JavaScript 中，返回的值將如下所示。

js
homogeneousToCartesian([10, 4, 5, 0]);

這等於：[Infinity, Infinity, Infinity]。

此齊次座標表示無窮遠處的某個點。這是一種方便地表示從原點沿特定方向射出的光線的方法。除了光線之外，它還可以被認為是方向向量的表示。如果此齊次座標與帶有平移的矩陣相乘，則平移實際上被去除。

當計算機上的數字非常大（或非常小）時，它們會變得越來越不精確，因為用於表示它們的 1 和 0 的數量有限。對較大數字執行的操作越多，結果中積累的錯誤就越多。當除以 w 時，這可以透過對兩個可能較小、較不易出錯的數字進行操作來有效地提高非常大數字的精度。

使用齊次座標的最後一個好處是它們非常適合與 4x4 矩陣相乘。頂點必須至少匹配矩陣的一個維度才能與之相乘。4x4 矩陣可用於編碼各種有用的變換。實際上，典型的透視投影矩陣使用 w 分量的除法來實現其變換。

裁剪空間中點和多邊形的裁剪髮生在齊次座標轉換回笛卡爾座標（透過除以 w）之前。這個最終空間被稱為歸一化裝置座標或 NDC。

要開始嘗試這個想法，可以修改之前的示例以允許使用 w 分量。除了修改 data，還要記住將 vertexAttribPointer() 更改為使用 4 個分量（第二個 size 引數）而不是 3 個。

js
// Redefine the triangles to use the W component
// prettier-ignore
const data = new Float32Array([
  // Triangle 1
  settings.left, settings.bottom, settings.depth, settings.w,
  settings.right, settings.bottom, settings.depth, settings.w,
  settings.left, settings.top, settings.depth, settings.w,

  // Triangle 2
  settings.left, settings.top, settings.depth, settings.w,
  settings.right, settings.bottom, settings.depth, settings.w,
  settings.right, settings.top, settings.depth, settings.w,
]);

然後頂點著色器使用傳入的 4 維點。

glsl
attribute vec4 position;

void main() {
  gl_Position = position;
}

首先，我們在中間繪製一個紅色框，但將 W 設定為 0.7。當座標除以 0.7 時，它們都將被放大。

js
box.draw({
  top: 0.5, // y
  bottom: -0.5, // y
  left: -0.5, // x
  right: 0.5, // x
  w: 0.7, // w - enlarge this box

  depth: 0, // z
  color: [1, 0.4, 0.4, 1], // red
});

現在，我們在上方繪製一個綠色框，但透過將 w 分量設定為 1.1 來縮小它。

js
box.draw({
  top: 0.9, // y
  bottom: 0, // y
  left: -0.9, // x
  right: 0.9, // x
  w: 1.1, // w - shrink this box

  depth: 0.5, // z
  color: [0.4, 1, 0.4, 1], // green
});

最後一個框未被繪製，因為它超出裁剪空間。深度超出 -1.0 到 1.0 的範圍。

js
box.draw({
  top: 1, // y
  bottom: -1, // y
  left: -1, // x
  right: 1, // x
  w: 1.5, // w - Bring this box into range

  depth: -1.5, // z
  color: [0.4, 0.4, 1, 1], // blue
});

結果

練習

  • 嘗試這些值，看看它們如何影響螢幕上渲染的內容。請注意，透過設定藍色框的 w 分量，之前被裁剪的藍色框如何重新回到範圍內。
  • 嘗試建立一個超出裁剪空間的新框，並透過除以 w 將其帶回。

模型變換

直接將點放置在裁剪空間中的用途有限。在實際應用中，你不會所有源座標都已經位於裁剪空間座標中。因此，大多數情況下，你需要將模型資料和其他座標轉換到裁剪空間。簡單的立方體是說明如何做到這一點的一個簡單示例。立方體資料由頂點位置、立方體面的顏色以及構成單個多邊形的頂點位置順序（以 3 個頂點為一組來構建組成立方體面的三角形）組成。位置和顏色儲存在 GL 緩衝區中，作為屬性發送到著色器，然後單獨進行操作。

最後計算並設定單個模型矩陣。此矩陣表示對構成模型的每個點執行的變換，以便將其移動到正確的空間，並對模型中的每個點執行任何其他所需的變換。這不僅適用於每個頂點，還適用於模型每個表面上的每個點。

在這種情況下，對於動畫的每一幀，一系列縮放、旋轉和平移矩陣將資料移動到裁剪空間中的所需位置。立方體的大小與裁剪空間相同（從 -1,-1,-1 到 1,1,1），因此需要將其縮小，以免完全填充裁剪空間。此矩陣在 JavaScript 中預先乘法後直接傳送到著色器。

以下程式碼示例定義了 CubeDemo 物件上的一個方法，該方法將建立模型矩陣。新函式看起來像這樣（實用函式在Web 的矩陣數學章節中介紹）

js
function computeModelMatrix(now) {
  // Scale down by 20%
  const scaleMatrix = scale(0.2, 0.2, 0.2);
  // Rotate a slight tilt
  const rotateXMatrix = rotateX(now * 0.0003);
  // Rotate according to time
  const rotateYMatrix = rotateY(now * 0.0005);
  // Move slightly down
  const translateMatrix = translate(0, -0.1, 0);
  // Multiply together, make sure and read them in opposite order
  this.transforms.model = multiplyArrayOfMatrices([
    translateMatrix, // step 4
    rotateYMatrix, // step 3
    rotateXMatrix, // step 2
    scaleMatrix, // step 1
  ]);
}

為了在著色器中使用它，它必須設定為統一位置。統一變數的位置儲存在下面所示的 locations 物件中。

js
this.locations.model = gl.getUniformLocation(webglProgram, "model");

最後將統一變數設定到該位置。這將矩陣傳遞給 GPU。

js
gl.uniformMatrix4fv(
  this.locations.model,
  false,
  new Float32Array(this.transforms.model),
);

在著色器中，每個位置頂點首先被轉換成齊次座標（一個 vec4 物件），然後與模型矩陣相乘。

glsl
gl_Position = model * vec4(position, 1.0);

注意：在 JavaScript 中，矩陣乘法需要自定義函式，而在著色器中，它內置於語言中，使用簡單的 * 運算子。

完整的編排程式碼是隱藏的。同樣，如果你感興趣，請點選本節中程式碼塊上的“播放”檢視。

結果

此時，變換後的點的 w 值仍然是 1.0。立方體仍然沒有任何透視。下一節將採用此設定並修改 w 值以提供一些透視。

練習

  • 使用縮放矩陣縮小框，並將其放置在裁剪空間中的不同位置。
  • 嘗試將其移出裁剪空間。
  • 調整視窗大小，觀察框如何變形。
  • 新增 rotateZ 矩陣。

除以 W

要開始對我們的立方體模型獲得一些透視效果，一個簡單的方法是將 Z 座標複製到 w 座標。通常，當將笛卡爾點轉換為齊次座標時，它會變成 (x,y,z,1)，但我們將其設定為類似於 (x,y,z,z)。實際上，我們希望確保檢視中的點 z 大於 0，因此我們將透過將值更改為 ((1.0 + z) * scaleFactor) 進行輕微修改。這將使通常在裁剪空間中（-1 到 1）的點根據比例因子設定移動到更像（0 到 1）的空間。比例因子會改變最終的 w 值，使其整體更高或更低。

著色器程式碼如下所示。

glsl
// First transform the point
vec4 transformedPosition = model * vec4(position, 1.0);

// How much effect does the perspective have?
float scaleFactor = 0.5;

// Set w by taking the z value which is typically ranged -1 to 1, then scale
// it to be from 0 to some number, in this case 0-1.
float w = (1.0 + transformedPosition.z) * scaleFactor;

// Save the new gl_Position with the custom w component
gl_Position = vec4(transformedPosition.xyz, w);

結果

看到那個面向攝像機的小三角形了嗎？這是它出現時的截圖。

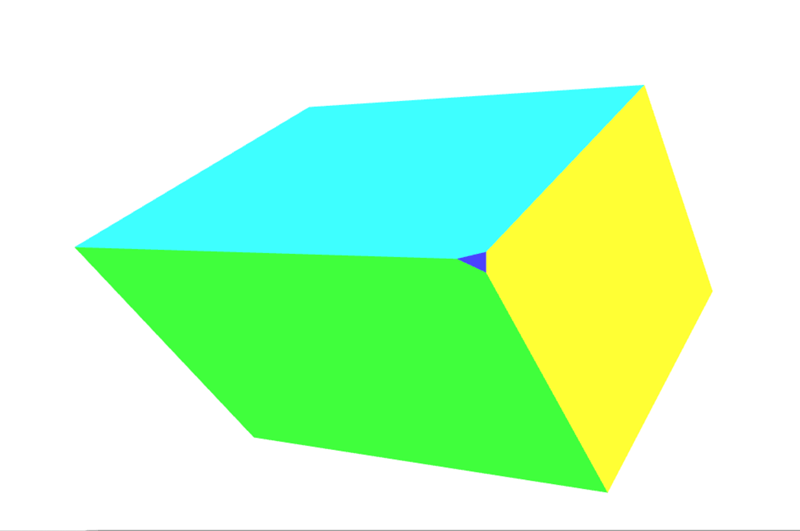
A small triangle appears in the top right corner

這是我們物件上新增的另一個面，因為我們形狀的旋轉導致該角延伸到裁剪空間之外，從而導致該角被裁剪掉。有關如何使用更復雜的矩陣來幫助控制和防止裁剪的介紹，請參閱下面的透視投影矩陣。

練習

如果這聽起來有點抽象，開啟頂點著色器並調整比例因子，看看它如何使頂點更多地向表面收縮。完全改變 w 分量的值，以獲得真正奇特的空間表示。

在下一節中，我們將把 Z 複製到 w 插槽的這一步變成一個矩陣。

簡單投影

填充 w 分量的最後一步實際上可以透過一個簡單的矩陣來完成。從單位矩陣開始。

js
// prettier-ignore
const identity = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, 0,
  0, 0, 0, 1,
];

multiplyPoint(identity, [2, 3, 4, 1]);
// [2, 3, 4, 1]

然後將最後一列的 1 向上移動一個位置。

js
// prettier-ignore
const copyZ = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, 1,
  0, 0, 0, 0,
];

multiplyPoint(copyZ, [2, 3, 4, 1]);
// [2, 3, 4, 4]

然而，在最後一個例子中，我們執行了 (z + 1) * scaleFactor。

js
const scaleFactor = 0.5;

// prettier-ignore
const simpleProjection = [
  1, 0, 0, 0,
  0, 1, 0, 0,
  0, 0, 1, scaleFactor,
  0, 0, 0, scaleFactor,
];

multiplyPoint(simpleProjection, [2, 3, 4, 1]);
// [2, 3, 4, 2.5]

再進一步分解一下，我們可以看到這是如何工作的。

js
const x = 2 * 1 + 3 * 0 + 4 * 0 + 1 * 0;
const y = 2 * 0 + 3 * 1 + 4 * 0 + 1 * 0;
const z = 2 * 0 + 3 * 0 + 4 * 1 + 1 * 0;
const w = 2 * 0 + 3 * 0 + 4 * scaleFactor + 1 * scaleFactor;

最後一行可以簡化為

js
const w = 4 * scaleFactor + 1 * scaleFactor;

然後提取 scaleFactor，我們得到這個

js
const w = (4 + 1) * scaleFactor;

這與我們上一個例子中使用的 (z + 1) * scaleFactor 完全相同。

在立方體演示中，添加了一個額外的 computeSimpleProjectionMatrix() 方法。該方法在 draw() 方法中被呼叫，並將比例因子傳遞給它。結果應該與上一個示例相同。

js
function computeSimpleProjectionMatrix(scaleFactor) {
  // prettier-ignore
  this.transforms.projection = [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, scaleFactor,
    0, 0, 0, scaleFactor,
  ];
}

儘管結果相同，但這裡的重要步驟在頂點著色器中。它不是直接修改頂點，而是乘以一個額外的投影矩陣，它（顧名思義）將 3D 點投影到 2D 繪圖表面。

glsl
// Make sure to read the transformations in reverse order
gl_Position = projection * model * vec4(position, 1.0);

結果

視錐體

在我們繼續討論如何計算透視投影矩陣之前，我們需要引入視錐體（也稱為檢視截錐體）的概念。這是當前使用者可見的空間區域。它是由視野以及指定為最近和最遠應渲染內容距離定義的 3D 空間區域。

在渲染時，我們需要確定哪些多邊形需要渲染以表示場景。這就是視錐體所定義的。但視錐體到底是什麼？

截錐體是將任何實體用兩個平行平面切掉兩個部分後形成的 3D 實體。考慮我們的相機，它正在檢視一個從鏡頭正前方開始並延伸到遠處的區域。可見區域是一個四面金字塔，其頂點位於鏡頭處，其四邊對應於其周邊視覺範圍的範圍，其底部位於它能看到的最遠距離處，就像這樣：

A depiction of the entire viewing area of a camera. This area is a four-sided pyramid with its peak at the lens and its base at the world's maximum viewable distance.

如果我們將此用於確定每幀要渲染的多邊形，我們的渲染器將需要渲染此金字塔內的每個多邊形，一直到無窮遠，包括那些非常靠近鏡頭——可能太近而無用（當然包括那些如此之近以至於真實人類無法在同一設定中聚焦的東西）——的多邊形。

所以減少我們需要計算和渲染的多邊形數量的第一步，我們將這個金字塔變成視錐體。我們將用來切除頂點以減少多邊形數量的兩個平面是近裁剪平面和遠裁剪平面。

在 WebGL 中，近裁剪平面和遠裁剪平面是透過指定從鏡頭到垂直於視線的平面上最近點的距離來定義的。任何比近裁剪平面更靠近鏡頭或比遠裁剪平面更遠的東西都將被移除。這導致了視錐體，它看起來像這樣：

A depiction of the camera's view frustum; the near and far planes have removed part of the volume, reducing the polygon count.

每幀要渲染的物件集基本上是透過從場景中所有物件的集合開始建立的。然後將完全在視錐體之外的任何物件從集合中移除。接下來，部分伸出視錐體之外的物件透過丟棄完全在視錐體之外的任何多邊形，以及裁剪穿過視錐體外部的多邊形，使其不再超出視錐體，從而被裁剪。

完成這些後，我們就有了完全在視錐體內的最大多邊形集。這個列表通常會透過背面剔除（移除背面朝向相機的多邊形）和使用隱藏表面判定的遮擋剔除（移除因為被更靠近鏡頭的多邊形完全遮擋而無法看到的多邊形）等過程進一步減少。

透視投影矩陣

到目前為止，我們已經一步步地建立了自己的 3D 渲染設定。然而，我們目前構建的程式碼存在一些問題。首先，每當我們調整視窗大小時，它都會變形。另一個問題是我們的簡單投影無法處理場景資料的廣泛值範圍。大多數場景無法在裁剪空間中工作。定義與場景相關的距離將有助於避免在轉換數字時丟失精度。最後，能夠精確控制哪些點放置在裁剪空間內部和外部非常有用。在之前的示例中，立方體的角偶爾會被裁剪掉。

透視投影矩陣是一種投影矩陣，它滿足所有這些要求。其數學運算也開始變得更復雜，並且不會在這些示例中完全解釋。簡而言之，它結合了除以 w（如之前的示例所示）和基於相似三角形的一些巧妙操作。如果你想閱讀其背後數學的完整解釋，請檢視以下連結：

關於下面使用的透視投影矩陣，一個重要的注意事項是它翻轉了 z 軸。在裁剪空間中，z+ 遠離觀察者，而使用此矩陣時，它向觀察者靠近。

翻轉 z 軸的原因是裁剪空間座標系是左手座標系（其中 z 軸指向遠離觀察者並進入螢幕），而數學、物理和 3D 建模以及 OpenGL 中的檢視/眼睛座標系的慣例是使用右手座標系（z 軸指向螢幕外並朝向觀察者）。更多資訊請參閱相關維基百科文章：笛卡爾座標系、右手定則。

讓我們看看 perspective() 函式，它計算透視投影矩陣。

js
function perspective(fieldOfViewInRadians, aspectRatio, near, far) {
  const f = 1.0 / Math.tan(fieldOfViewInRadians / 2);
  const rangeInv = 1 / (near - far);

  // prettier-ignore
  return [
    f / aspectRatio, 0, 0, 0,
    0, f, 0, 0,
    0, 0, (near + far) * rangeInv, -1,
    0, 0, near * far * rangeInv * 2, 0,
  ];
}

此函式的四個引數是

fieldOfViewInRadians（視場角，以弧度表示）

一個以弧度表示的角度，指示觀察者一次可以看到多少場景。數字越大，相機可見的越多。邊緣的幾何形狀變得越來越扭曲，相當於一個廣角鏡頭。當視場角越大時，物體通常會變小。當視場角越小，相機在場景中看到的就越少。物體受透視的影響扭曲得更少，物體看起來更接近相機。

aspectRatio

場景的縱橫比，相當於其寬度除以其高度。在這些示例中，它是視窗寬度除以視窗高度。此引數的引入最終解決了畫布調整大小和重塑時模型變形的問題。

nearClippingPlaneDistance

一個正數，表示螢幕內到垂直於地面的平面的距離，任何比此平面更近的物體都將被裁剪掉。這在裁剪空間中對映為 -1，不應設定為 0。

farClippingPlaneDistance

一個正數，表示超出此平面幾何體將被裁剪掉的距離。這在裁剪空間中對映為 1。此值應保持與幾何體距離合理接近，以避免渲染時出現精度誤差。

在最新版本的立方體演示中，computeSimpleProjectionMatrix() 方法已被 computePerspectiveMatrix() 方法替換。

js
function computePerspectiveMatrix() {
  const fieldOfViewInRadians = Math.PI * 0.5;
  const aspectRatio = window.innerWidth / window.innerHeight;
  const nearClippingPlaneDistance = 1;
  const farClippingPlaneDistance = 50;

  this.transforms.projection = perspective(
    fieldOfViewInRadians,
    aspectRatio,
    nearClippingPlaneDistance,
    farClippingPlaneDistance,
  );
}

著色器程式碼與之前的示例相同。

glsl
gl_Position = projection * model * vec4(position, 1.0);

此外（未顯示），模型的位移和縮放矩陣已更改，以將其移出裁剪空間並進入更大的座標系。

結果

練習

  • 試驗透視投影矩陣和模型矩陣的引數。
  • 將透視投影矩陣替換為使用正交投影。在 MDN WebGL 共享程式碼中，你會找到 MDN.orthographicMatrix()。這可以替換 CubeDemo.prototype.computePerspectiveMatrix() 中的 MDN.perspectiveMatrix() 函式。

檢視矩陣

雖然一些圖形庫有一個可以在組合場景時定位和指向的虛擬攝像機，但 OpenGL（以及 WebGL）沒有。這就是檢視矩陣發揮作用的地方。它的任務是平移、旋轉和縮放場景中的物件，以便它們相對於觀察者（給定觀察者的位置和方向）位於正確的位置。

模擬相機

這利用了愛因斯坦狹義相對論的一個基本方面：參照系和相對運動原理指出，從觀察者的角度來看，你可以透過對場景中的物件施加相反的變化來模擬改變觀察者的位置和方向。無論哪種方式，結果對觀察者來說都是相同的。

想象一個盒子放在桌子上，一個相機放在離盒子一米遠的地方，對準盒子，盒子的正面朝向相機。然後想象將相機移離盒子，直到它兩米遠（透過在相機的 Z 位置上增加一米），然後將其向左滑動 10 釐米。盒子從相機處後退這麼多，並稍微向右滑動，從而在相機看來變小，並向相機暴露其左側的一小部分。

現在讓我們重置場景，將盒子放回其起始位置，相機距盒子兩米遠，並直接面向盒子。然而，這次相機被固定在桌子上，無法移動或轉動。這就是 WebGL 中的工作方式。那麼我們如何模擬相機在空間中的移動呢？

我們不是將相機向後和向左移動，而是對盒子應用逆變換：我們將盒子向後移動一米，然後向右移動 10 釐米。從這兩個物件的角度來看，結果是相同的。

所有這些的最後一步是建立檢視矩陣，它轉換場景中的物件，使它們定位以模擬相機的當前位置和方向。我們現有的程式碼可以在世界空間中移動立方體並投影所有內容以具有透視，但我們仍然無法移動相機。

想象一下用物理相機拍攝電影。你擁有幾乎可以隨意放置相機並向任何方向瞄準相機的自由。為了在 3D 圖形中模擬這一點，我們使用檢視矩陣來模擬物理相機的位置和旋轉。

與直接變換模型頂點的模型矩陣不同，檢視矩陣移動的是一個抽象的相機。實際上，頂點著色器仍然只移動模型，而“相機”保持不動。為了使其正常工作，必須使用變換矩陣的逆矩陣。逆矩陣實際上是反轉變換，所以如果我們向前移動相機檢視，逆矩陣會導致場景中的物體向後移動。

以下 computeViewMatrix() 方法透過向內和向外、向左和向右移動檢視矩陣來對其進行動畫處理。

js
function computeViewMatrix(now) {
  const moveInAndOut = 20 * Math.sin(now * 0.002);
  const moveLeftAndRight = 15 * Math.sin(now * 0.0017);

  // Move the camera around
  const position = translate(moveLeftAndRight, 0, 50 + moveInAndOut);

  // Multiply together, make sure and read them in opposite order
  this.transforms.view = multiplyArrayOfMatrices([
    // Exercise: rotate the camera view
    position,
  ]);
}

著色器現在使用三個矩陣。

glsl
gl_Position = projection * view * model * vec4(position, 1.0);

在此步驟之後，GPU 管道將裁剪超出範圍的頂點，並將模型傳送到片段著色器進行光柵化。

結果

關聯座標系

此時，退一步看看並標記我們使用的各種座標系將是有益的。首先，立方體的頂點在模型空間中定義。為了在場景中移動模型。這些頂點需要透過應用模型矩陣轉換為世界空間。

模型空間 → 模型矩陣 → 世界空間

相機還沒有做任何事情，這些點需要再次移動。目前它們在世界空間中，但需要將它們移動到檢視空間（使用檢視矩陣）以表示相機放置。

世界空間 → 檢視矩陣 → 檢視空間

最後，需要新增一個投影（在我們的例子中是透視投影矩陣），以便將世界座標對映到裁剪空間座標。

檢視空間 → 投影矩陣 → 裁剪空間

練習

  • 在場景中移動相機。
  • 在檢視矩陣中新增一些旋轉矩陣以環顧四周。
  • 最後，跟蹤滑鼠的位置。使用 2 個旋轉矩陣，根據使用者滑鼠在螢幕上的位置，使相機上下看。

另見

幫助改進 MDN

瞭解如何貢獻

此頁面最後由MDN 貢獻者於修改。

在 GitHub 上檢視此頁面 • 報告此內容問題
© . Content available under a Creative Commons license.