3D 碰撞檢測 - 遊戲開發

軸對齊包圍盒

與 2D 碰撞檢測一樣，**軸對齊包圍盒** (AABB) 是確定兩個遊戲實體是否重疊的最快演算法。它包括將遊戲實體包裹在一個不旋轉（因此軸對齊）的盒子中，並檢查這些盒子在 3D 座標空間中的位置，以檢視它們是否重疊。

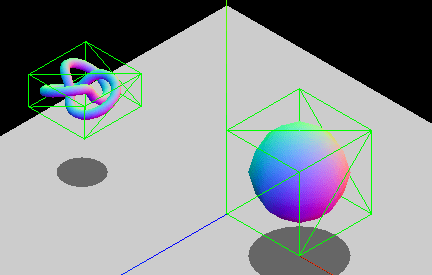
Two 3-D non-square objects floating in space encompassed by virtual rectangular boxes.

出於效能原因，存在**軸對齊約束**。兩個不旋轉盒子之間的重疊區域可以透過純邏輯比較來檢查，而旋轉盒子則需要額外的三角函式運算，計算速度較慢。如果您的實體會旋轉，您可以修改包圍盒的尺寸，使其仍然包裹物件，或者選擇使用其他包圍幾何體型別，例如球體（它們不受旋轉影響）。下面的動畫 GIF 展示了一個 AABB 動態調整大小以適應旋轉實體的圖形示例。該盒子不斷改變尺寸以緊密貼合內部的實體。

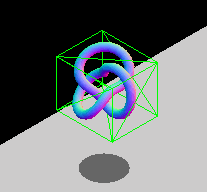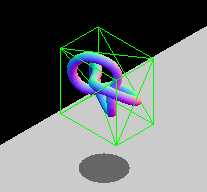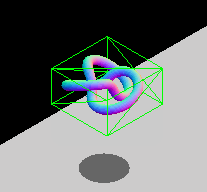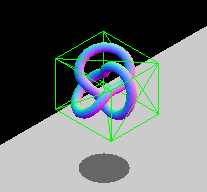
Animated rotating knot showing the virtual rectangular box shrink and grow as the knots rotates within it. The box does not rotate.

注意： 請參閱使用 Three.js 進行包圍體碰撞檢測文章，瞭解此技術的實際實現。

點 vs. AABB

檢查一個點是否在 AABB 內非常簡單——我們只需檢查點的座標是否落在 AABB 內；分別考慮每個軸。如果我們假設 P_x、P_y 和 P_z 是點的座標，而 B_minX–B_maxX、B_minY–B_maxY 和 B_minZ–B_maxZ 是 AABB 每個軸的範圍，我們可以使用以下公式計算兩者之間是否發生了碰撞：

f(P, B)= (P_x \ge B_{minX} \wedge P_x \le B_{maxX}) \wedge (P_y \ge B_{minY} \wedge P_y \le B_{maxY}) \wedge (P_z \ge B_{minZ} \wedge P_z \le B_{maxZ})

或者在 JavaScript 中：

function isPointInsideAABB(point, box) {
  return (
    point.x >= box.minX &&
    point.x <= box.maxX &&
    point.y >= box.minY &&
    point.y <= box.maxY &&
    point.z >= box.minZ &&
    point.z <= box.maxZ
  );
}

AABB vs. AABB

檢查一個 AABB 是否與另一個 AABB 相交與點測試類似。我們只需要對每個軸進行一次測試，使用盒子的邊界。下圖展示了我們在 X 軸上執行的測試——基本上，範圍 A_minX–A_maxX 和 B_minX–B_maxX 是否重疊？

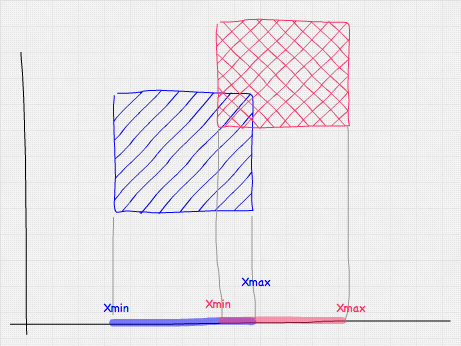
Hand drawing of two rectangles showing the upper right corner of A overlapping the bottom left corner of B, as A's largest x coordinate is greater than B's smallest x coordinate.

從數學上講，這看起來是這樣的：

f(A, B) = (A_{minX} \le B_{maxX} \wedge A_{maxX} \ge B_{minX}) \wedge ( A_{minY} \le B_{maxY} \wedge A_{maxY} \ge B_{minY}) \wedge (A_{minZ} \le B_{maxZ} \wedge A_{maxZ} \ge B_{minZ})

在 JavaScript 中，我們會這樣做：

function intersect(a, b) {
  return (
    a.minX <= b.maxX &&
    a.maxX >= b.minX &&
    a.minY <= b.maxY &&
    a.maxY >= b.minY &&
    a.minZ <= b.maxZ &&
    a.maxZ >= b.minZ
  );
}

包圍球

使用包圍球進行碰撞檢測比 AABB 稍微複雜一些，但仍然相當快速。球體的優點在於它們不受旋轉影響，因此如果被包裹的實體旋轉，包圍球仍然是相同的。它們的主要缺點是，除非它們包裹的實體實際上是球形的，否則包裹通常不合適（例如，用包圍球包裹一個人會產生大量誤報，而 AABB 會是更好的匹配）。

點 vs. 球

要檢查一個球體是否包含一個點，我們需要計算點與球體中心之間的距離。如果該距離小於或等於球體的半徑，則該點在球體內部。

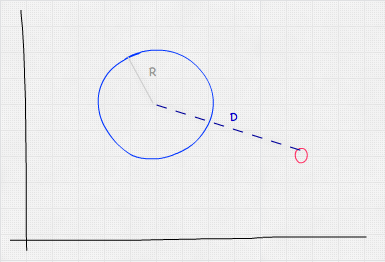
Hand drawing of a 2D projection of a sphere and a point in a Cartesian coordinate system. The point is outside of the circle, to the lower right of it. The distance is denoted by a dashed line, labeled D, from the circle's center to the point. A lighter line shows the radius, labeled R, going from the center of the circle to the border of the circle.

考慮到兩點 A 和 B 之間的歐幾里得距離為： $\sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2}$ ，我們的點與球體碰撞檢測公式將如下所示：

f(P,S) = S_{radius} \ge \sqrt{(P_x - S_x)^2 + (P_y - S_y)^2 + (P_z - S_z)^2}

或者在 JavaScript 中：

function isPointInsideSphere(point, sphere) {
  // we are using multiplications because is faster than calling Math.pow
  const distance = Math.sqrt(
    (point.x - sphere.x) * (point.x - sphere.x) +
      (point.y - sphere.y) * (point.y - sphere.y) +
      (point.z - sphere.z) * (point.z - sphere.z),
  );
  return distance < sphere.radius;
}

注意： 上面的程式碼包含一個平方根，計算成本可能很高。一個簡單的最佳化方法是比較平方距離與平方半徑，因此最佳化後的方程將涉及 distanceSqr < sphere.radius * sphere.radius。

球 vs. 球

球體與球體測試與點與球體測試類似。我們需要測試的是球體中心之間的距離是否小於或等於它們半徑之和。

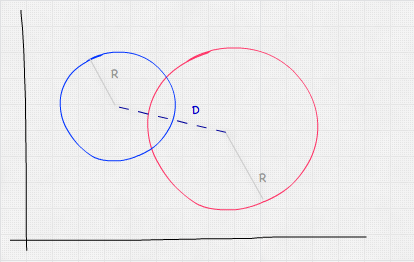
Hand drawing of two partially overlapping circles. Each circle (of different sizes) has a light radius line going from its center to its border, labeled R. The distance is denoted by a dotted line, labeled D, connecting the center points of both circles.

從數學上講，這看起來像：

f(A,B) = \sqrt{(A_x - B_x)^2 + (A_y - B_y)^2 + (A_z - B_z)^2} \le A_{radius} + B_{radius}

或者在 JavaScript 中：

function intersect(sphere, other) {
  // we are using multiplications because it's faster than calling Math.pow
  const distance = Math.sqrt(
    (sphere.x - other.x) * (sphere.x - other.x) +
      (sphere.y - other.y) * (sphere.y - other.y) +
      (sphere.z - other.z) * (sphere.z - other.z),
  );
  return distance < sphere.radius + other.radius;
}

球 vs. AABB

測試球體和 AABB 是否碰撞稍微複雜一些，但仍然簡單快捷。一個合乎邏輯的方法是檢查 AABB 的每個頂點，並對每個頂點進行點與球體測試。然而，這有點大材小用——測試所有頂點是不必要的，因為我們只需要計算 AABB 的最近點（不一定是頂點）與球體中心之間的距離，看看它是否小於或等於球體的半徑。我們可以透過將球體的中心限制到 AABB 的範圍內來獲得這個值。

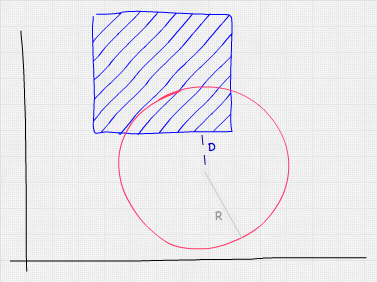
Hand drawing of a square partially overlapping the top of a circle. The radius is denoted by a light line labeled R. The distance line goes from the circle's center to the closest point of the square.

在 JavaScript 中，我們會這樣進行測試：

function intersect(sphere, box) {
  // get box closest point to sphere center by clamping
  const x = Math.max(box.minX, Math.min(sphere.x, box.maxX));
  const y = Math.max(box.minY, Math.min(sphere.y, box.maxY));
  const z = Math.max(box.minZ, Math.min(sphere.z, box.maxZ));

  // this is the same as isPointInsideSphere
  const distance = Math.sqrt(
    (x - sphere.x) * (x - sphere.x) +
      (y - sphere.y) * (y - sphere.y) +
      (z - sphere.z) * (z - sphere.z),
  );

  return distance < sphere.radius;
}

使用物理引擎

3D 物理引擎提供了碰撞檢測演算法，其中大多數也基於包圍體。物理引擎的工作方式是建立一個物理體，通常附加到其視覺表示上。該身體具有速度、位置、旋轉、扭矩等屬性，以及一個物理形狀。這個形狀是碰撞檢測計算中考慮的因素。

我們準備了一個即時碰撞檢測演示（附帶原始碼），您可以檢視以瞭解這些技術的實際應用——它使用了開源的 3D 物理引擎 cannon.js。

另見

MDN 上的相關文章

外部資源

幫助改進 MDN

瞭解如何貢獻

此頁面最後修改於 2025 年 7 月 11 日，由 MDN 貢獻者編輯。

在 GitHub 上檢視此頁面 • 報告此內容的問題